Q. Find the length of the tangent from a point M which is at a distance of 17 cm from the centre O of the circle of radius 8 cm.
Since, MN is the tangent of the circle,
∠MNO = 90⁰
⟹ MO2 = MN2 + ON2
⟹ 172 = MN2 + 82
⟹ 289 = MN2 + 64
⟹ 289 – 64 = MN2
⟹ MN2 = 225
⟹ MN = 15
Thus, the length of the tangent is 15 cm.
Q. If the common difference of an A.P. is 3, then find a20 – a15.
Sol.
Let the first term of the AP be a.
an = a(n − 1)d
a20 – a15 = [a + (20 – 1)d] – [a + (15 – 1)d]
= 19d – 14d
= 5d
= 5 × 3=15
.question Solve the following system of linear equations by substitution method:
2x – y = 2
x + 3y =1
Here, 2x – y = 2
⟹ y = 2x – 2
⟹ x + 3y = 15
Substituting the value of y from (i) in (ii), we get
x + 6x – 6 = 15
⟹ 7x = 21
⟹ x = 3
From (i), y = 2 × 3 – 2 = 4
∴ x = 3 and y = 4
Q. From a rectangular sheet of paper ABCD with AB = 40 cm and AD = 28 cm, a semi-circular portion with BC as diameteris cut off. Find the area of remining paper (use π = 22/7)
Length of paper, AB = l = 40cm
Width of paper, AD = b = 40cm
Area of paper = l × b = 40 × 28 = 1120 cm2
Diameter of semi-circle = 28cm
∴ Radius of semi-circle, r = 14cm
Thus, area of semi-circle = 1/2. πr2
= 1/2 × 22/7 × 14 × 14
= 308cm2
∴ Area of remaining paper = 1120 – 308 = 812 cm2
Q. The sum of the 4th and 8th terms of an AP is 24 and the sum of the 6th and 10th term is 44. Find the first three terms of the AP.
Sol.
Given that sum of the 4th and 8th terms of an AP is 24.
⟹ a + 3d + a + 7d = 24
⟹ 2a + 10d = 24 ...(i)
Also the sum of the 6th and 10th term is 44.
⟹ a + 5d + a + 9d = 44
⟹ 2a + 14d = 44 ...(ii)
Subtracting equation (i) from equation (ii), we get:
4d = 20
⟹ d = 5
Substituting d = 5 in equation (i), we have:
2a + 10d = 24
⟹ 2a + 10 (5) = 24
⟹ 2a + 50 = 24
⟹ 2a = −26
⟹ a = −13
Hence first term of given A.P. is −13 and common difference is 5.
Q. The taxi charges in a city comprise of a fixed charge together with the charges for the distance covered. For a journey of 10 km the charge paid is Rs. 75 and for a journey of 15 km the charge paid is Rs. 110.
(i) What will a person have to pay for travelling a distance of 25 km?
(ii)Which mathematical concept is used in this question?
(iii) What is its value?
Sol.
Let the fixed charge of taxi be Rs. x per km and the running charge be ` y per km.
According to the question,
x + 10y = 75
x + 15y = 110
Subtracting equation (ii) from equation (i), we get
– 5y = – 35
⟹ y = 7
Putting y = 7 in equation (i), we get x = 5
∴Total charges for travelling a distance of 25 km = x + 25y
= (5 + 25 × 7)
= (5 + 175)
= 180
Q. A motor boat whose speed is 24 km/hr in still water takes 1 hr more to go 32km upstream than to return downstream to the same spot. Find the speed of the stream.
Sol.
Let the speed of stream be x.
Then,
Speed of boat in upstream is 24 ‒ x
In downstream, speed of boat is 24 + x
According to question,
Time taken in the upstream journey ‒ Time taken in the downstream journey = 1 hour
Q. The first and the last terms of an AP are 10 and 361 respectively. If its common difference is 9 then find the number of terms and their total sum?
Sol.
Given, first term, a = 10
Last term, al = 361
And, common difference, d = 9
Now al =a + (n −1) ⟹ 361 = 10 + (n − 1)9
⟹ 361 = 10 + 9n − 9
⟹ 361 = 9n + 1
⟹ 9n = 360
⟹ n = 40
⟹ 361 = 10 + 9n − 9
⟹ 361 = 9n + 1
⟹ 9n = 360
⟹ n = 40
Therefore, total number of terms in AP = 40
Now, sum of total number of terms of an AP is given as:
Sn = n/2 [2a + (n − 1)d]
⟹ S40 = 40/2 [2 × 10 + (40 − 1)9]
= 20|20 + 39 x 9]
=20[20 + 351]
=20 × 371 = 7420
⟹ S40 = 40/2 [2 × 10 + (40 − 1)9]
= 20|20 + 39 x 9]
=20[20 + 351]
=20 × 371 = 7420
Thus, sum of all 40 terms of AP = 7420


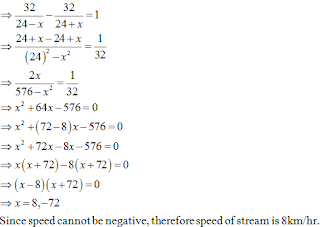
Comments
Post a Comment